• AI

機械学習による非階層型クラスタリング　（K-means法）

代表的なクラスタリングの手法には、

・階層 型 クラスタリング( Agglomerative Nesting( AGNES))

・非 階層 型 クラスタリング( K-means 法)

が挙げられますが、今回は、非階層型クラスタリング( K-means 法)を使ったアルゴリズムを、機械学習用のデータリポジトリにある「 Wholesale customers Data Set」で試してみました。　PythonではK-means法はscikit-leanのライブラリーを利用すれば簡単に実行できます。

以下のデータより卸売企業のグループ分けを行います。

＜サンプルデータ項目＞

Channel 仕入先（連続値でない）
Region 地域　（連続値でない）
Fresh 生鮮食品
Milk 乳製品
Grocery 食料雑貨品
Frozen 冷凍食品
Detergents_Paper 洗剤、紙製品
Delicatessen 惣菜

必要なライブラリーを読み込みます。

try:
    xrange
except NameError:
    xrange = range

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans, MiniBatchKMeans
from sklearn.metrics import silhouette_samples, silhouette_score
from sklearn.preprocessing import StandardScaler, MaxAbsScaler

%matplotlib inline

データを読み込み先頭の５行を表示します。

wholsesale_data = pd.read_csv('dataset/Wholesale_customers_data.csv')
wholsesale_data.head()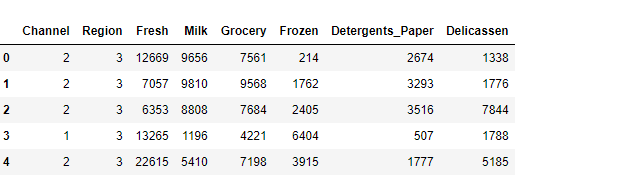
Image from Gyazo

Means法は連続値を想定しているため、カテゴリ―変数である ChannelとReginは外します。 （シードからデータ点までの距離を最小化するクラスタリングには使えない）

cols = ['Fresh', 'Milk', 'Grocery', 'Frozen', 'Detergents_Paper',
        'Delicassen']
dataset_for_cl = wholsesale_data[cols]
dataset_for_cl.head()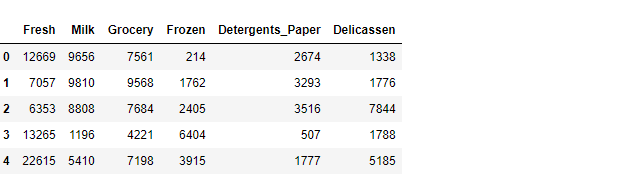
Image from Gyazo

ユークリッド距離に基づいてクラスタリングするので、スケーリングを行います。 　（最小値を０，最大値を1にして正規化します。）

scaler = MaxAbsScaler()
dataset_for_cl_scaled = scaler.fit_transform(dataset_for_cl)

Elbow Methodを使って最適なクラスター数を探してみます。

max_cluster = 10
clusters_ = range(1, max_cluster)
intra_sum_of_square_list = []
for k in clusters_:
    km = KMeans(n_clusters=k, init='k-means++', n_init=10, max_iter=300)
    km.fit(dataset_for_cl)
    intra_sum_of_square_list.append(km.inertia_)

# Elbow Methodによる描画
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.set_title('Elbow Method')
ax.set_xlabel('Number of Clutser')
ax.set_ylabel('Intra Sum of distances(WCSS)')
plt.plot(clusters_, intra_sum_of_square_list)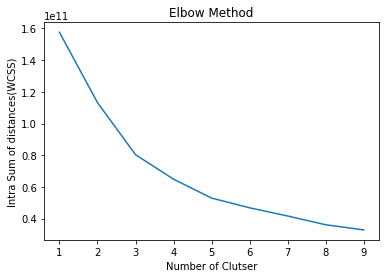
Image from Gyazo

WCSS（within-cluster sum of spuare）　目的関数が急激に減少しているのは、６のあたりですので、今回はクラスター数を６と判断します。

次に、シルエットプロットを表示します。

n_clusters = 6
km = KMeans(n_clusters=n_clusters, init='k-means++', n_init=10, max_iter=300)
km.fit(dataset_for_cl_scaled)
cluster_labels = km.predict(dataset_for_cl_scaled)

silhouette_avg = silhouette_score(dataset_for_cl_scaled, cluster_labels)

each_silhouette_score = silhouette_samples(dataset_for_cl_scaled,
                                           cluster_labels, metric='euclidean')

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

y_lower = 10

for i in range(n_clusters):
        ith_cluster_silhouette_values = \
         each_silhouette_score[cluster_labels == i]
        ith_cluster_silhouette_values.sort()
        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i

        color = colorlist[i]
        ax.fill_betweenx(np.arange(y_lower, y_upper), 0,
                         ith_cluster_silhouette_values,
                         facecolor=color, edgecolor=color, alpha=0.3)

        # Label the silhouette plots with their cluster numbers at the middle
        ax.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

        # Compute the new y_lower for next plot
        y_lower = y_upper + 10  # 10 for the 0 samples

ax.set_title('Silhouette plot')
ax.set_xlabel('Silhouette score')
ax.set_ylabel('Cluster label')

# The vertical line for average silhouette score of all the values
ax.axvline(x=silhouette_avg, color='red', linestyle='--')

ax.set_yticks([])  # Clear the yaxis labels / ticks
ax.set_xticks([-0.2, 0, 0.2, 0.4, 0.6, 0.8, 1])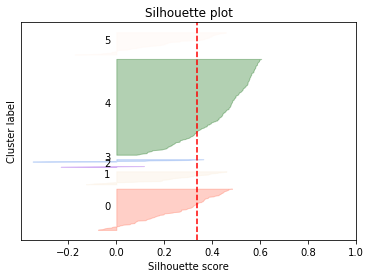
Image from Gyazo

クラスター4が大きくなっていますので、クラスター分けが最適かどうかはこの時点では、判断がむずかしいところです。

最後にデータを可視化して検討してみます。

km_centers = pd.DataFrame(km.cluster_centers_, columns=cols)
km_centers.plot.bar(ylim=[0, 2], fontsize=10)
km_centers
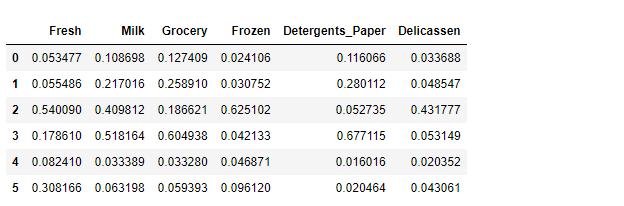
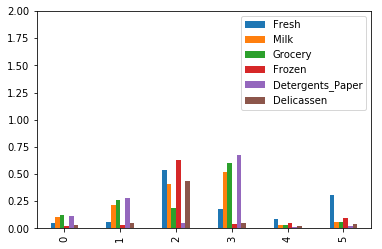
Image from Gyazo Image from Gyazo

問題のクラスター4ですが、どの商品カテゴリーも差がなく特徴がないクラスターになっている事がわかります。　クラスター2とクラスター3はボリュームは小さいですが、商品の仕入れに関して特徴があるといえる結果となりました。

機械学習のK-means法を使えば、コンピュータが面倒な計算を行って、クラスタリング（似たものを集めてくる）結果を導きだしてくれますが、結局のところデータの準備から計算方法の検討まで人間の判断が必要であり、試行錯誤も伴います。　なにより、ビジネスにどのように活用するかは、そのゴールを事前にすり合わせておくことが最も大切でしょう。

PAGE TOP